1. 자기회귀(AutoRegression, AR) 모형t라는 시점의 값은 이전 시점 n개에 의해 설명될 수 있음을 의미한다.
(n개의 다른 가중치를 가진다.)
적절한 n값을 결정하기 위해서 부분자기상관함수를 사용한다.
ts(): 수치형 벡터를 시계열 자료로 전환
> rate<-c(1072, 1081, 1090, 1065, 1087, 1085, 1130, 1130, 1122, 1122, 1144, 1121, 1131, 1129, 1137, 1146, 1176, 1194, 1174, 1200, 1224, 1213, 1172, 1197)
> rate_ts<-ts(rate)
#2회의 차분을 실시하여 진행(평규이 일정하지 않아서 정상성이 만족하지 않음)
> rate_ts_diff2<-diff(rate_ts, differences=2)
> pacf(rate_ts_diff2)
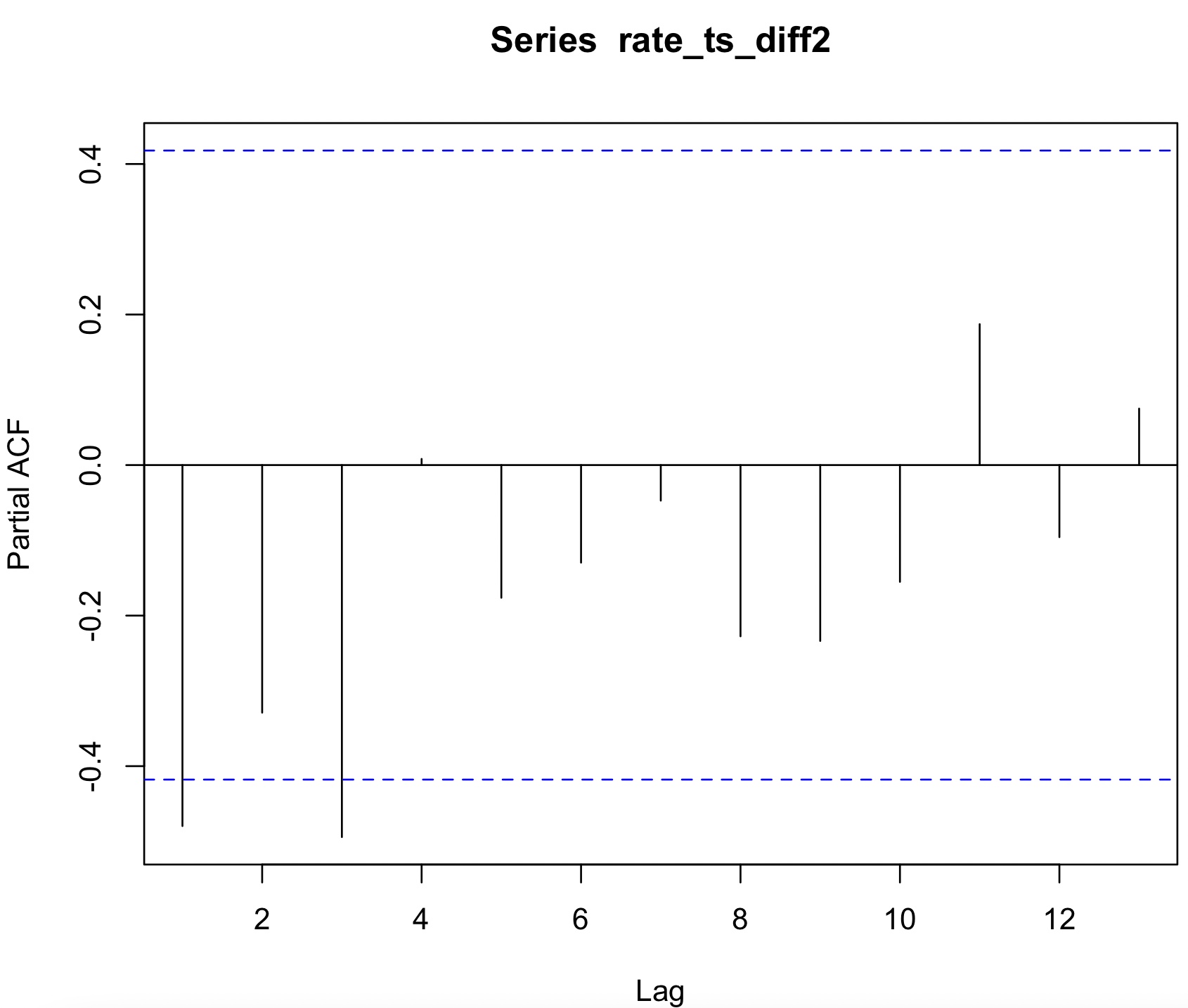
pacf 그래프를 통해서 시차가 2인 지점에서 처음으로 파란선 안에 존재한다.
(시차가 2인 지점부터 자기상관이 낮음)
시차가 4인점부터 급격하게 자기상관이 낮다.(바로전인 시차가 3인 지점까지 현재 시점에 영향을 미친다.)
위에서 AR(1)과 AR(3)이 가능한 후보 모형이다.
2. 이동평균(Moving Average, MA) 모형자기회귀 모형이 이전 시점들의 자료값들에 의한 선형결합이라면,
이동평균 모형은 이전 시점의 백색 잡음들의 선형결합으로 표현할 수 있다.
백색잡음들의 선형결합으로 이루어져 있기 때문에 항상 정상성을 만족한다.
적절한 n의 값을 결정하기 위해서 자기상관함수를 사용한다.
#정산성 가정이 필요하지 않으므로, 차분 없이 진행
> rate<-c(1072, 1081, 1090, 1065, 1087, 1085, 1130, 1130, 1122, 1122, 1144, 1121, 1131, 1129, 1137, 1146, 1176, 1194, 1174, 1200, 1224, 1213, 1172, 1197)
> rate_ts<-ts(rate)
> acf(rate_ts)
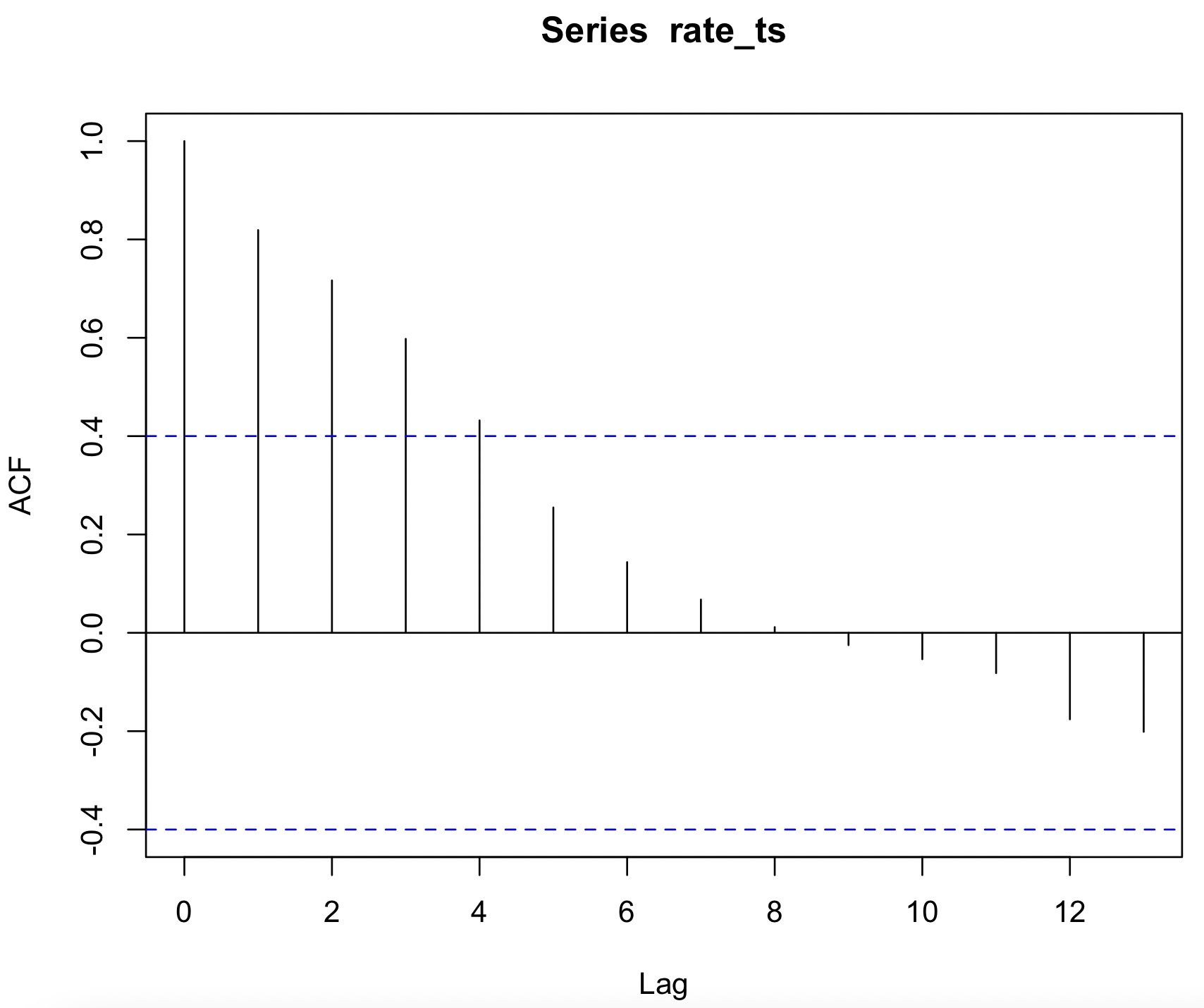
acf 그래프에서 시차가 5인 지점에서 처음으로 파란선안에 존재한다.
(시차가 5인 지점부터 자기 상관이 낮다.)
바로 전 시차 4지점까지 현재 시점에 영향을 미친다고 판단한다.
MA(4) 모형 사용이 적절하다.
3. 자기회귀누적이동평균 모형(AutoRegression Integrated Moving Average, ARIMV)비정상 시계열을 다룰 수 있는 모형으로 현실에 존재하는 대부부의 시계열 자료를 설명할 수 있다.
비정상 시계열이기 때문에 차분이나, 변환을 통해 정상화할 수 있다.
이상적인 p, d, q 값을 찾아야 한다.
p: AR 모형의 차수
d: 시계열 자료를 정상화하기 위한 필요 차분 횟수
q: MA 모형의 차수
p=0이면 IMA(d, q) 모형
d=0이면 ARMA(p, q) 모형
q=0이면 ARI(d, q) 모형
install.packages(‘forecast’, depedencies=T)
install.packages(‘xts’)
auto.arima() 함수를 이용해서 최적의 모형을 구할수 있다.(forecast packages)
> rate<-c(1072, 1081, 1090, 1065, 1087, 1085, 1130, 1130, 1122, 1122, 1144, 1121, 1131, 1129, 1137, 1146, 1176, 1194, 1174, 1200, 1224, 1213, 1172, 1197)
> rate_ts<-ts(rate)
> library(forecast)
Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
> auto.arima(rate_ts)
Series: rate_ts
ARIMA(0,1,0)
sigma^2 estimated as 431.7: log likelihood=-102.41
AIC=206.83 AICc=207.02 BIC=207.96
최적 모형은 ARIMA(0, 1, 0)이다.(정상성을 위해 1회 차분이 필요)
# 1회 차분 실시 후, 자기상관함수와 부분자기상관함수 확인
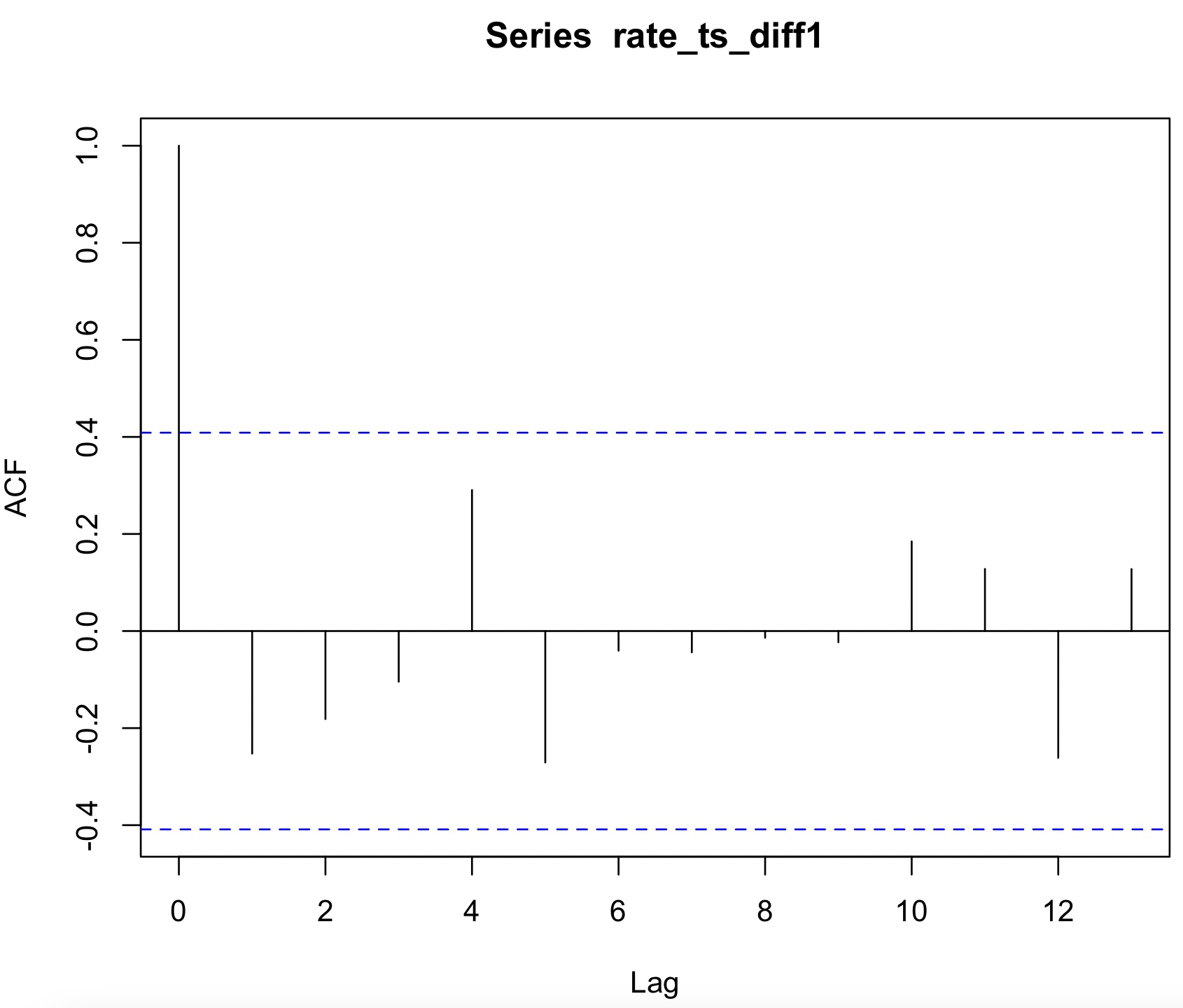
> rate_ts_diff1<-diff(rate_ts, differences=1)
> acf(rate_ts_diff1)
시차가 1인 지점에서 처음으로 파란선 안에 존재한다.
시차가 1인 지점부터는 자기상관이 낮다.
즉 1회 차분시 AR(0), MA(0)이 되는 것을 확인할 수 있다.
1회 차분하여 정상성을 만족하는 자료는 이전 시점에 영향을 받지 않는 무작위 변동이다.